Logik
| ∧ | AND |
| ∨ | OR |
| ⇒ | IF...THEN... |
| ↑ | NAND |
| ↓ | NOR |
Relation
| Reflexiv | An jedem Knoten gibt es eine Schlinge a <–> a |
| Symmetrisch | Wenn es a –> b gibt muss es auch b –> a geben |
| Antisymmetrisch | Höchstens ein Pfeil zwischen zwei Knoten |
| Asymmetrisch | Antisymmetrisch und keine Schlingen |
| Transitiv | Wenn es a –> b und b –> c gibt muss es auch a –> c geben. |
| Äquivalenzrelation | Wenn reflexiv, symmetrisch & transitiv |
| Partiell | Wenn reflexiv, antisymmetrisch & transitiv |
Kombinatorik
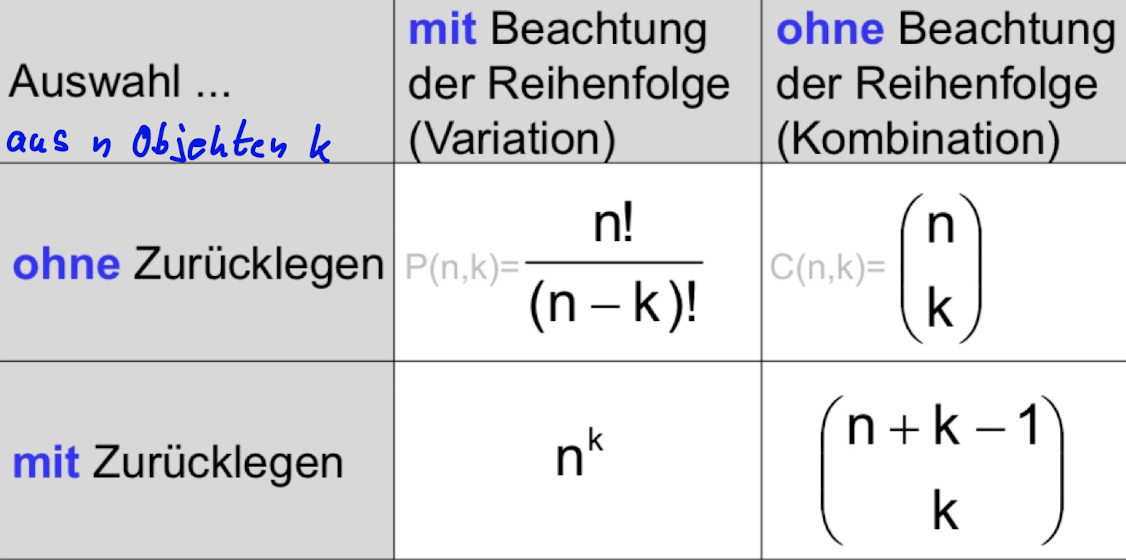
| Multiplizieren | aufeinanderfolende Schritte kombinieren |
| Addieren (+) | gegenseitig ausschließende Möglichkeiten zusammenzählen |
| Subtrahieren (-) | ungültige Möglichkeiten voneinander abziehen |
| Dividieren | gleich Große Gruppen aufteilen |
Graphentheorie
| Planar | Graph bei dem sich Kanten nicht kreuzen |
| Inzidenzmatrix | Knoten und Kanten werden nummeriert |
| Hamilton-Kreis | Jeder Knoten ist genau einmal enthalten |
| Euler-Zug | Alle Knoten haben geraden Grad |
| Kantenzug | Knoten die durchlaufen werden, werden nacheinander angegeben. |
| geschlossener Kreis | Start == Ende |
| Weg | Alle Knoten im Kantenzug sind unterschiedlich |
| Kreis | Alle Knoten sind unterschiedlich und Start == Ende |
Vektorräume, Normen, Matrizen & lineare Abbildungen
| Länge/Betrag | \( \parallel \vec{v} \parallel = \sqrt{a_1^2 + a_2^2 + \ldots} \) |
| Einheitsvektor | \( \frac{\vec{v}}{\parallel \vec{v} \parallel}\) |
| Skalarprodukt | \( <\vec{a},\vec{b}> = a_1*b_1+a_2*b_2+...\) |